As a teenager, I have developed a theory of “fractional sums” — a way to extend the definition of sums like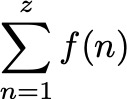 
to non-integer numbers z. It turns out that there is an essentially unique way of doing so, for a large class of functions f, if one demands that the usual calculation rules for sum series and a certain continuity property remain valid. Not only does this extend all well-known identitites for finite sums (such as the geometric or binomial series, sums of polynomials, and the interpolation of the factorial by the Gamma function), but it also produces many interesting and beautiful relations to special functions and constants that are invisible in the case of integer z. See the formula gallery below for a selection.
I won the first prize in mathematics in the German youth science competition “Jugend forscht” in 1998 with this work. In collaboration with Dierk Schleicher, this has led to a number of publications:
- M. Müller and D. Schleicher, How to Add a Noninteger Number of Terms: From Axioms to New Identities, Am. Math. Mon. 118(2), 136-152 (2011). DOI:10.4169/amer.math.monthly.118.02.136; arXiv:1001.4695.
- M. Müller and D. Schleicher, Fractional sums and Euler-like identities, Ramanujan J. 21, 123-143 (2010). DOI:10.1007/s11139-009-9214-9; arXiv:math/0502109.
- M. Müller and D. Schleicher, How to add a non-integer number of terms, and how to produce unusual infinite summations, J. Comp. Appl. Math. 178, 347-360 (2005). DOI:10.1016/j.cam.2004.08.009.
Formula Gallery
A few years after discovering the first of the equations below, I rediscovered it in the works of Leonhard Euler.
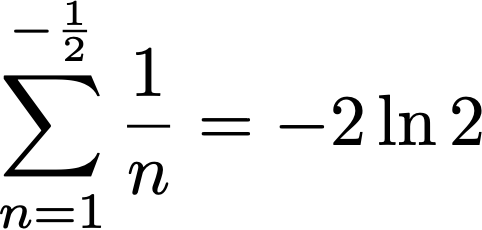
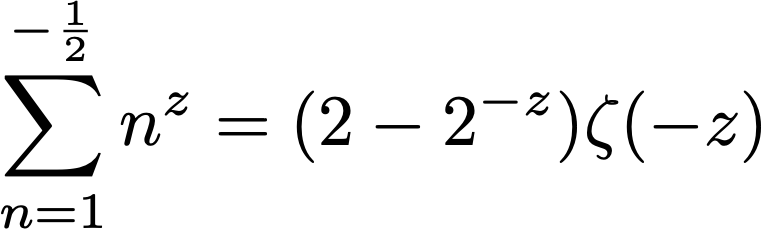
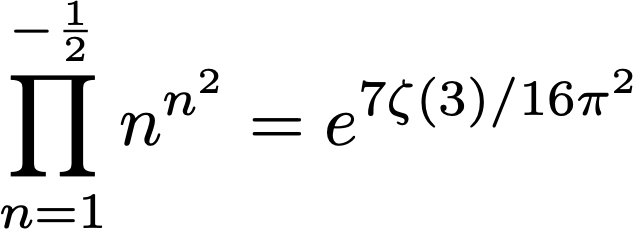
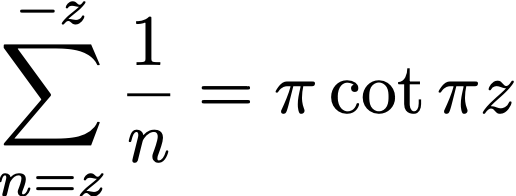
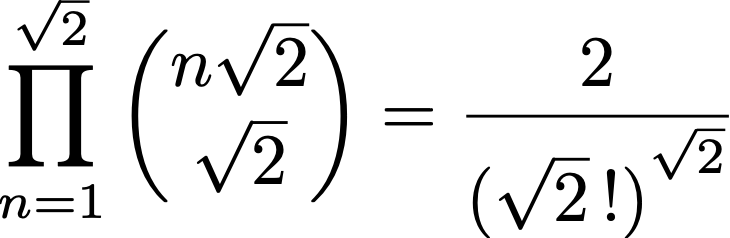
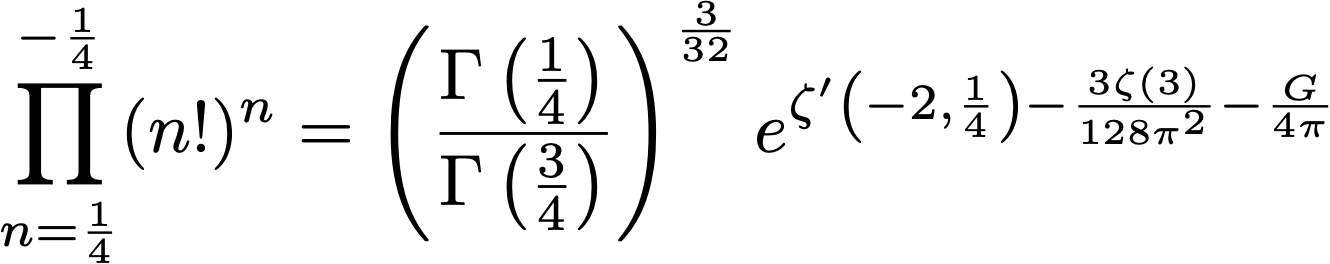
Note that γ=0.577215… is the Euler-Mascheroni constant, G=0.91596… is the Catalan constant, and ζ denotes the Riemann and Hurwitz zeta functions.
Some identities look simple in fractional sums form, but can be written as highly non-trivial infinite series and limits, like the following:
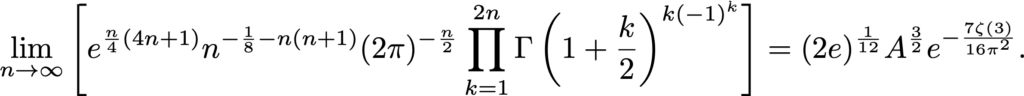
In this equation, A=1.282427… denotes the Glaisher-Kinkelin constant.
Here are some further identities related to special functions and constants, including complex summation boundaries:
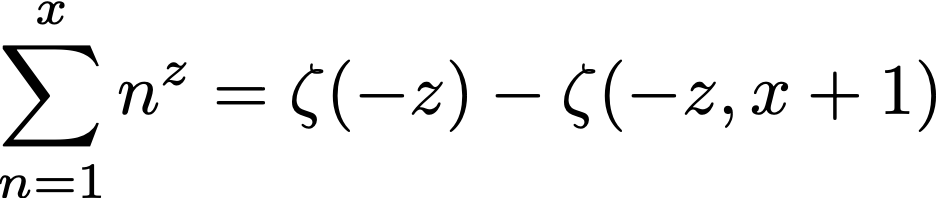
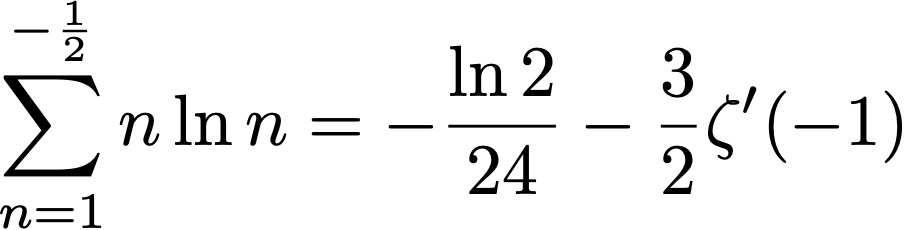
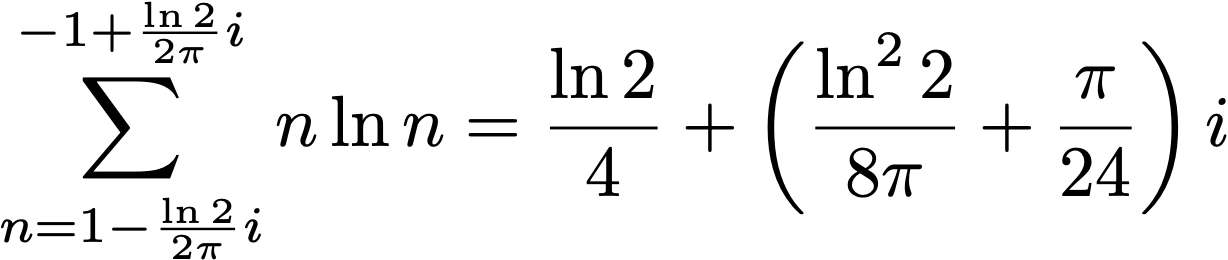
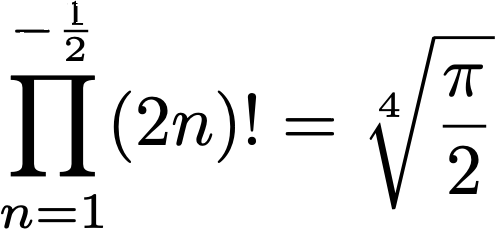
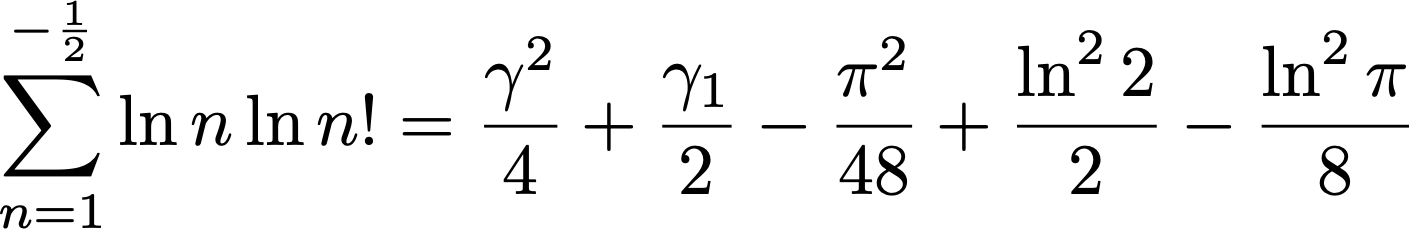
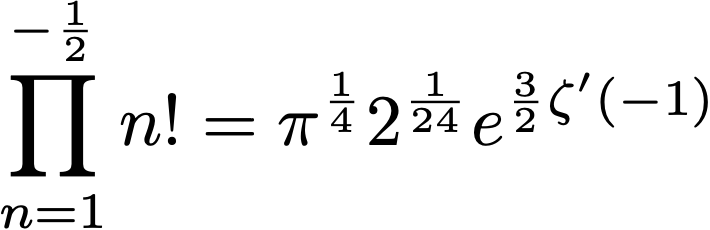
Here, γ1=0.072815… is one of the Stieltjes’ constants, and the final product at the bottom right is related to Barnes’ double gamma function.
There has been some follow-up work by other researchers (and our work Hamiltonian for the Zeros of the Riemann Zeta Function has been resulting from the above, see this note for how), but I am not any more working on this topic.