See also the Talks and Publications pages.
Quantum Information and Foundations of Physics
We study the Foundations of Physics from an information-theoretic perspective. The main tool and inspiration is Quantum Information Theory, which we apply to a variety of questions: Can we derive the abstract formalism of quantum theory from simple principles? How can we test quantum theory against more general alternatives, under minimal assumptions? What is the nature of reality and our place in it?
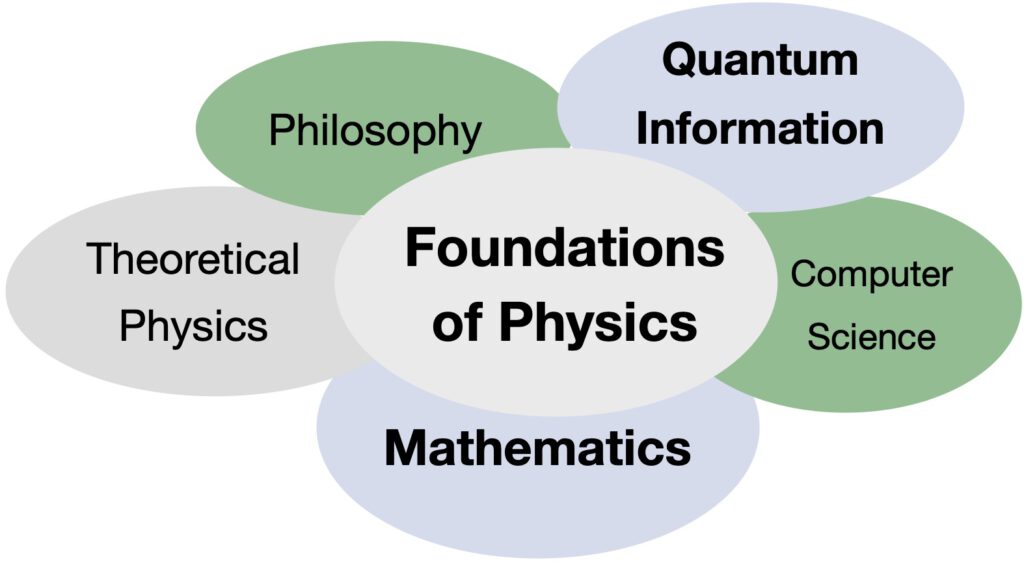
Aiming for complete mathematical rigor and conceptual clarity, our research touches mathematics, physics, computer science, and philosophy. Proving theorems with pen and paper, we are arguably Mathematical Physicists.
Vision
Quantum theory challenges our view of the world: Bell’s Theorem proves that it is inconsistent to think that there is a single, material world with well-defined properties that just “sits there” and reveals its properties to us when we make observations, unless we give up some other important principles of physics. Our intuitions about the universe and our place in it seem to be deeply misguided. But what exactly is it that quantum physics teaches us about reality?
I believe that the most fruitful and accurate way to look at physics and its foundations is through the lens of information theory. In this view, we should not think of our world as being composed, fundamentally, of material things that move and collide, but of immaterial structure. Quantum information is our currently most accurate mathematical description of this structure. Its most fruitful and explanatorily powerful interpretation is in terms of a “catalog of probabilities”: the quantum state is the thing that gives someone the probabilities of its future observations. Not only does this view dissolve the measurement problem (a “collapse” is simply an update of probabilities in the light of new information), but it motivates and nourishes a particular path towards understanding reality. In my own research, it has led me to pursue, for example, the following research directions:
- Reconstructions of Quantum Theory. Quantum theory is one of our most successful physical theories, but its standard textbook formulation is mysterious. For example, why are states described by complex vectors in a Hilbert space, and why do observables correspond to self-adjoint operators? In the last few years, my colleagues and I have shown (based on pioneering work by Lucien Hardy) that the formalism of quantum theory can be reconstructed from simple information-theoretic principles, without presupposing any of the usual mathematical machinery. This is conceptually similar to the derivation of the Lorentz transformations from the principles and relativity and the constancy of the speed of light.
Note that this formalism starts without assuming that there is something like an operator algebra, or amplitudes, or any other ingredients of the usual mathematical formalism. Instead, these properties are rigorously and non-trivially derived from the information-theoretic principles. - Resource-Theoretic Approach to Thermodynamics. In this approach, thermodynamics is not seen as a theory about, say, the statistical properties of the evolution of a large ensemble of gas particles, but as a theory that describes the constraints faced by an agent who plays a “game” against nature. Namely, if an experimenter is constrained by reversible time evolution and energy conservation, then what kinds of transformations can they perform on their physical system? It turns out that this “resource-theoretic” approach can be used to put the known laws of thermodynamics on rigorous mathematical and conceptual footing. For example, according to this view, it is immediately obvious that the information held by an agent impacts its ability to, say, extract energy, which makes insights like Landauer’s Principle much less surprising. Moreover, this approach leads to proofs of the standard laws of thermodynamics, and also to surprising refinements as they apply to “small” quantum systems without going to the thermodynamic limit.
- Testing Quantum Theory. Could physics be “even weirder” than quantum? The above reasoning suggests that quantum theory is only one possible probabilistic theory among many others. This view leads to new proposals for experimental tests of quantum theory (and, indirectly, to progress on understanding quantum information): design experiments that probe its probabilistic structure, but that do so in a theory-agnostic way without presupposing any particular alternative. An example approach can be found in this paper, where we have recently suggested a scheme for experimentally testing quantum theory that can — as a by-product — also be used to certify the nonclassicality of physical systems. Putting this into actual practice is the content of a current project funded by the FWF.
- Algorithmic Idealism. Why is there a world with simple laws of nature that seems to have begun in a simple initial state? How should we think of the simulation hypothesis, the Boltzmann brain problem, the duplication or computer simulation of observers, or death? The fact that there is no clear consensus on these questions shows that there is something important about the nature of reality and our place in it that we have not yet understood. Algorithmic Idealism is a theory that I’ve proposed that attempts to answer all these questions in a unified way. It is neither algorithmic nor a form of idealism (because consciousness does not play a direct role in it), but it begins with the premise that the first-person perspective (the “self”) is in some precise sense fundamental, not the third-person perspective (the world). It comes in different mathematical formulations, based on algorithmic information theory, and is work in progress.
Some concepts developed in our group
We use mathematics not only to solve concrete problems, but sometimes suggest creative new concepts that allow us to look at the foundations of physics from new angles. For example, our group has discovered the phenomenon of correlated catalysis, which has since become a prominent tool in quantum information theory. Here is a cloud of some concepts we developed:
Topics and Projects
Please see my group homepage at IQOQI Vienna for some description of current research topics. And here is is a list of recent (after 2021) third-party-funded projects (for earlier projects, please see my CV page):
Relational and operational quantum physics in spacetime
There is currently a large wave of interest in applying relational and operational methods from quantum information and foundations to quantum field theory (QFT). Our proposal will apply two current topics of research from the foundations of quantum theory (QT) to QFT: Quantum reference frames (QRFs), and generalized probabilistic theories (GPTs). But rather than beginning with a fully developed version of QFT and studying its predictions (as other works do), our approach will analyze how probabilistic systems can be relativistically covariant in the most general way, and build a QRF-based version of important parts of QFT from the ground up that is relational by construction. Learn more
Generalized Contextuality in Large Quantum Systems
Quantum theory promises technological applications that would be impossible within classical physics: faster computation, more accurate metrology, or the generation of provably secure random numbers. However, to make this work, we first need to test whether our devices are really quantum and work as desired a task called certification. This is not only relevant for technology, but also for fundamental physics: given some large physical system, such as a Bose-Einstein condensate, how can we prove that its properties cannot be explained by classical physics? In other words, how can we certify its nonclassicality? In this project, we will develop a new method to do so, both theoretically (via mathematical proofs and conceptual argumentation) and experimentally (with concrete data supplied by colleagues at ETH Zurich). […] Learn more
Black-Box Quantum Information Under Spacetime Symmetries
Quantum theory has not only revolutionized our understanding of physics, but it has also led to a multitude of technological applications in information theory. For example, quantum physics admits unconditionally secure cryptography or the generation of provably random numbers. […] Previous research has focused on black boxes with abstract inputs and outputs, like abstract bits (zeros and ones) as commonly used in information theory. But in many actual experiments, the inputs and outputs are not abstract, but concrete spatiotemporal quantities such as the spatial direction of a magnetic field, the duration of a pulse, or the angle of a polarizer. The goal of this project is to theoretically analyze the foundations and applications of such spatiotemporal black boxes.[…] Learn more
Local Operations on Quantum Fields
The notion of locality is one of the most important concepts of science. In non-relativistic quantum mechanics, it is usually built into the formalism by demanding that composite systems compose with the tensor product.
In Quantum Field Theory (QFT), the rules of the game change: all operations act on the same Hilbert space, and space-like separated operations are required to commute (microcausality). However, as observed by Sorkin, microcausality alone does not exclude faster-than-light communication in experiments with more than two separate parties. In this regard, QFT is an incomplete physical theory: it still lacks a mathematical description of the most general operations that an experimenter can conduct within a finite space and in a finite time. […]
In this project, we aim to provide an explicit mathematical formulation of local operations for QFT and QG. […]
Joint project with Časlav Brukner, Borivoje Dakić, and Miguel Navascués. Learn more
Mathematical Models of Idealism and Dualism: an Adversarial Collaboration
The rationalist blog Slate Star Codex defines an “adversarial collaboration” as “an effort by two people with opposing opinions on a topic to collaborate on a summary of the evidence. The question on which the two applicants disagree is this: Does consciousness play a directly relevant role in quantum theory, in particular in the context of the measurement problem? Kelvin McQueen believes that the answer could well be “yes”: consciousness may be responsible for wave function collapse, in a way that can be described by explicit mathematical models. Markus Müller believes that the answer is “no”: quantum states represent propensities of an agent’s future records, and collapse is probabilistic update. […]
Joint project with Kelvin McQueen.
Former group members
- Andrew J. P. Garner (postdoc), now with the Austrian Institute of Technology.
- Marius Krumm (PhD student), now Postdoc at the University of Innsbruck.
- Philipp Höhn (postdoc), now Assistant Professor at Okinawa Institute of Science and Technology.
- Mark Francis Rogers (pre-university research student), now at the University of Manchester.
- Michele Pastena (PhD student), now Project Engineer with Safetec GmbH.
- Jakob Scharlau (Master student), now with dida Machine Learning.
- Michael Cuffaro (postdoc), now Alexander von Humboldt Fellow and external member of the Munich Center for Mathematical Philosophy.
- Adam Koberinski (Graduate Student Assistant), now Postdoctoral Fellow at the Rotman Institute of Philosophy.
- Jonathon Riddell (undergraduate “work study” student), now Research Fellow at the University of Birmingham.
- Nicole Yunger Halpern (PSI Master Student, Perimeter Institute for Theoretical Physics), now NIST physicist and Adjunct Assistant Professor of Physics and IPST at the University of Maryland, leading a Quantum Steampunk Laboratory.
- Emily Adlam (PSI Summer Student, Perimeter Institute), now Assistant Professor of Philosophy at Chapman University.