

I am a Research Group Leader at the Institute for Quantum Optics and Quantum Information (IQOQI) Vienna, a Lecturer at the University of Vienna, and a Visiting Fellow at the Perimeter Institute for Theoretical Physics in Waterloo, Canada. I am also an Associate Faculty member of the Rotman Institute of Philosophy.
My research is motivated by Wheeler’s “It From Bit” paradigm: to understand the foundations of physics, we have to take an information-theoretic perspective. I have worked on deriving quantum theory from simple principles, on the resource-theoretic approach to thermodynamics, and I have suggested a view (“Algorithmic Idealism”) in which not the external world, but a mathematical notion of the first person is fundamental (more topics and details below).

My research has led to several awards, including a Canada Research Chair, the Birkhoff-von Neumann prize, and ÖAW’s Best Paper Award. I am extremely grateful for the opportunity to work with a group of talented and enthusiastic young researchers at IQOQI Vienna. To contact me, write to markus.mueller (at-symbol) oeaw.ac.at.
Current research
- Working with Manuel Mekonnen, Stefan Ludescher, Thomas Galley and Jan Glowacki on quantum reference frames, compositionality, locality and gauge theories in our Quantum Science Austria project “Local operations on quantum fields”. In particular, we are interested in labelling-QRFs for indistinguishable particles and how this excludes parastatistics.
- Our FWF project “Generalized contextuality in large quantum systems” is progressing, with Albert Aloy, Caroline Jones, Thomas Galley, and our colleagues at ETH Zurich and ICTQT Gdańsk.
- Thinking about “Black-box quantum information under spacetime symmetries“, speed limits, and implications for generalized contextuality.
News and upcoming
- Jan 2025: substantially revised our Wigner’s Friend paper. Now with classical Frauchiger-Renner-like no-go theorem.
- Feb 2025: Welcome Jan Glowacki! New preprint “Invariance under quantum permutations rules out parastatistics”.
- April 2025: Quanta Magazine article about our work on quantum references frames and parastatistics.
- June 2025: New preprint “Certified randomness from quantum speed limits”.
Selected Talks and Podcasts
A list of all talks (with links to videos and slides) can be found on my Talks page.
Testing quantum theory by generalizing noncontextuality
Podcast with Karl Friston on my Algorithmic Idealism approach
Why do I propose this approach, how is it done, and what can it predict? I am grateful to Karl Friston and the Philosophy Babble team for the opportunity to discuss this with them.
Algorithmic idealism – what if the world is not fundamental?
Operational interpretation of entropy and free energy without the thermodynamic limit
See this PRX paper: In the resource-theoretic approach to thermodynamics, the Helmholtz free energy attains a surprising operational interpretation without any thermodynamic limit, for single small quantum systems.
Quantum theory and Jordan algebras from simple principles
Space, time and quantum probabilities: from fundamental insights to protocols
Is quantum theory the only probabilistic theory that “fits into space and time”? We analyze this by showing how QT fares in metrological games, via rotational correlations. For spins 0, 1/2, and 1, QT is “optimal”, but not for 3/2 and higher.
Selected Papers
All papers including Open Access links can be found on my Publications page.
On the significance of Wigner’s Friend in contexts beyond quantum foundations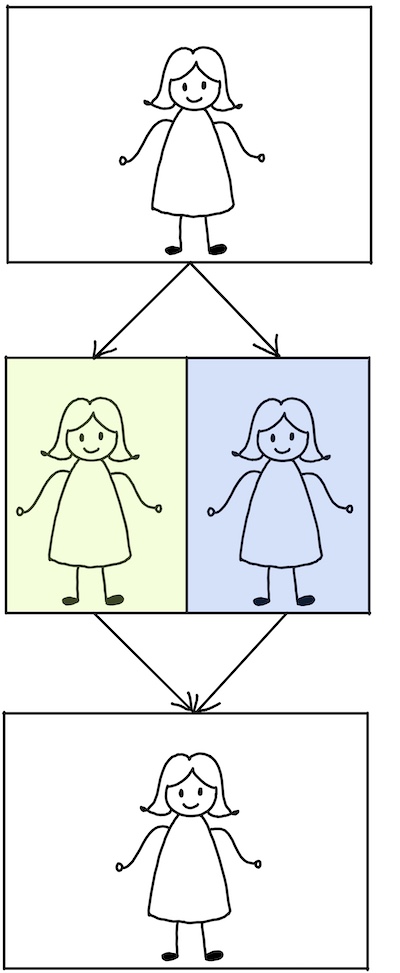 We argue that Wigner’s friend should be analyzed in a wider context, pointing at a current frontier of science beyond quantum foundations (“Restriction A”). To this end, we introduce a classical version of the Frauchiger-Renner paradox, and relate W.F. to several other puzzles in physics and philosophy.
We argue that Wigner’s friend should be analyzed in a wider context, pointing at a current frontier of science beyond quantum foundations (“Restriction A”). To this end, we introduce a classical version of the Frauchiger-Renner paradox, and relate W.F. to several other puzzles in physics and philosophy.
Correlating Thermal Machines and the Second Law at the Nanoscale I show that the Helmholtz free energy F has a physical interpretation without any averaging or thermodynamic limit: it determines the (im)possibility of state transitions of single, small quantum systems if the heat engine is allowed to become correlated or entangled with the work medium while preserving its own state.
I show that the Helmholtz free energy F has a physical interpretation without any averaging or thermodynamic limit: it determines the (im)possibility of state transitions of single, small quantum systems if the heat engine is allowed to become correlated or entangled with the work medium while preserving its own state.
A derivation of quantum theory from physical requirements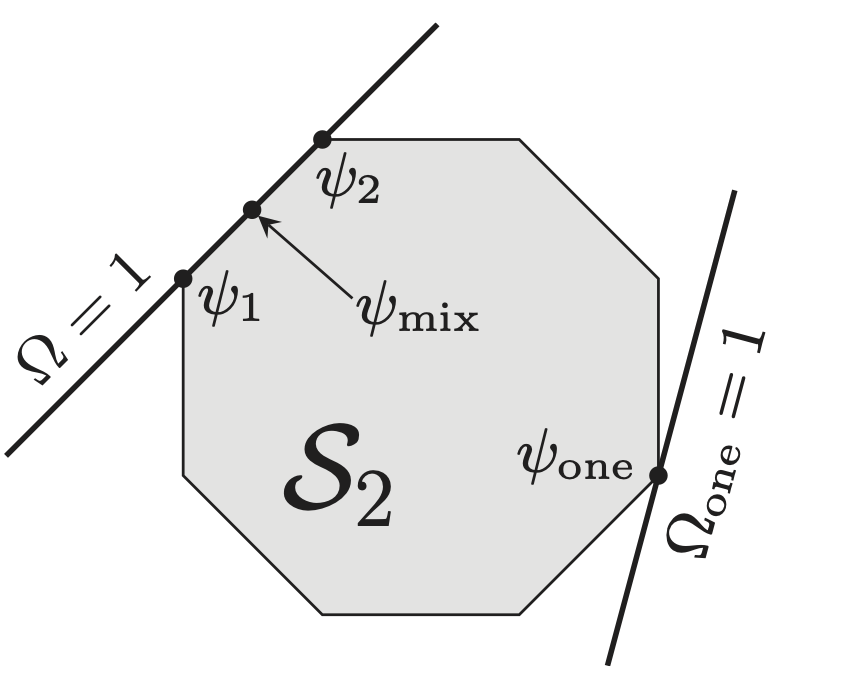 We derive the Hilbert space formalism of quantum theory from a few simple information-theoretic principles, without presupposing any of its mathematical machinery (such as operators or complex numbers). This solved a longstanding open problem in the field.
We derive the Hilbert space formalism of quantum theory from a few simple information-theoretic principles, without presupposing any of its mathematical machinery (such as operators or complex numbers). This solved a longstanding open problem in the field.
Quantum reference frame transformations as symmetries and the paradox of the 3rd particle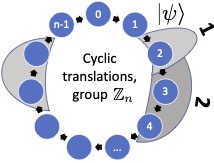 We give an axiomatic definition of QRF transformations for finite discrete translations. This resolves an apparent paradox from the literature with an algebraic treatment of how system composition should be understood under quantum symmetries.
We give an axiomatic definition of QRF transformations for finite discrete translations. This resolves an apparent paradox from the literature with an algebraic treatment of how system composition should be understood under quantum symmetries.
The quantum bit from relativity of simultaneity on an interferometer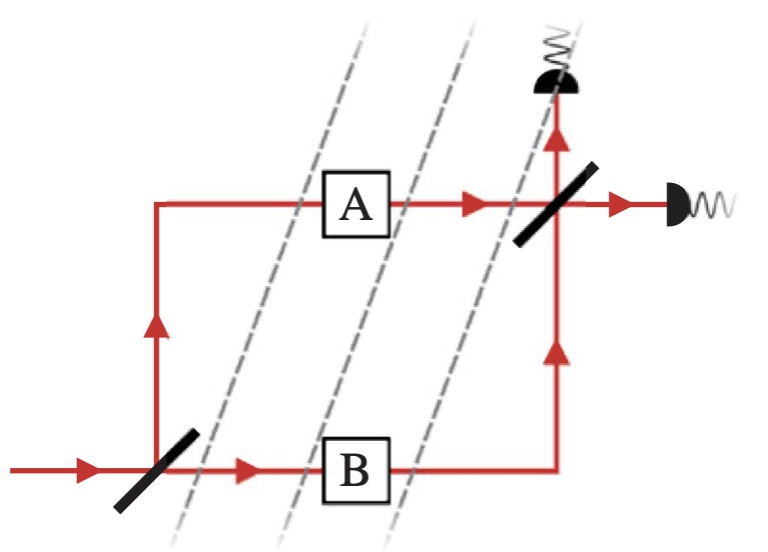 A simple thought experiment that shows a fundamental relation between spacetime and quantum theory: the qubit Bloch ball must be either 1-, 2-, 3- or 5-dimensional (i.e. classical, or quantum over the reals, complex numbers or quaternions) because of relativity of simultaneity.
A simple thought experiment that shows a fundamental relation between spacetime and quantum theory: the qubit Bloch ball must be either 1-, 2-, 3- or 5-dimensional (i.e. classical, or quantum over the reals, complex numbers or quaternions) because of relativity of simultaneity.
An operational approach to spacetime symmetries: Lorentz transformations from quantum communication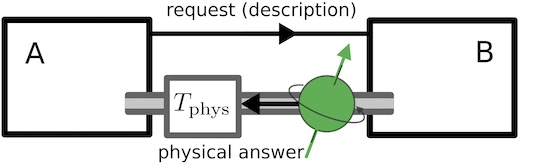 Usually, we think of spacetime symmetries as fundamental and implement them unitarily in quantum theory. Here we suggest that this reasoning can be reversed: communicating quantum laboratories must be related by an element of the Lorentz group merely due to the structure of quantum theory.
Usually, we think of spacetime symmetries as fundamental and implement them unitarily in quantum theory. Here we suggest that this reasoning can be reversed: communicating quantum laboratories must be related by an element of the Lorentz group merely due to the structure of quantum theory.
The black hole information problem beyond quantum theory We derive the Page curve (and the Hayden-Preskill results) for general probabilistic theories beyond quantum theory, rigorously and axiomatically. Black hole evaporation turns out to depend on an interference parameter r, where r=2 for QT.
We derive the Page curve (and the Hayden-Preskill results) for general probabilistic theories beyond quantum theory, rigorously and axiomatically. Black hole evaporation turns out to depend on an interference parameter r, where r=2 for QT.
Testing Quantum Theory by Generalizing Noncontextuality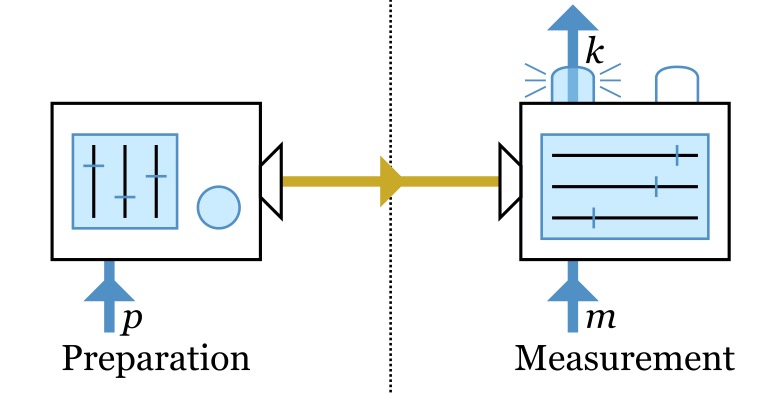 If Nature is fundamentally quantum, which effective statistics (for example, classical probabilities) can we plausibly expect to see in the lab? We give a complete answer to this question and use this to propose a novel experimental test of quantum theory.
If Nature is fundamentally quantum, which effective statistics (for example, classical probabilities) can we plausibly expect to see in the lab? We give a complete answer to this question and use this to propose a novel experimental test of quantum theory.
The measurement postulates of quantum mechanics are operationally redundant If unitary quantum mechanics leads to probabilities somehow, then these must be described by the Born rule. We give a particularly careful und rigorous proof of this, without hidden assumptions, deriving the Born and measurement update rules from the other postulates.
If unitary quantum mechanics leads to probabilities somehow, then these must be described by the Born rule. We give a particularly careful und rigorous proof of this, without hidden assumptions, deriving the Born and measurement update rules from the other postulates.
Coherence and Asymmetry Cannot be Broadcast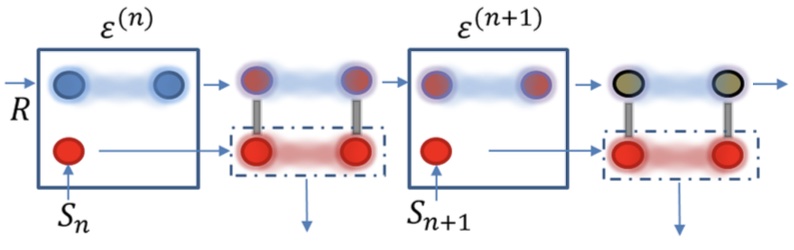 Coherence and asymmetry are valuable resources in quantum metrology and thermodynamics. Here we prove a general no-go theorem: they cannot be reused catalytically on any finite-dimensional system, even if we allow the generation of correlations or entanglement between the systems.
Coherence and asymmetry are valuable resources in quantum metrology and thermodynamics. Here we prove a general no-go theorem: they cannot be reused catalytically on any finite-dimensional system, even if we allow the generation of correlations or entanglement between the systems.
Structure of Reversible Computation Determines the Self-Duality of Quantum Theory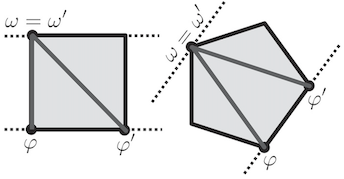 Quantum theory has the remarkable feature of self-duality: states and measurement outcomes are described (up to normalization) by the exact same mathematical objects. Here, we prove that this feature is a consequence of bit symmetry: any probabilistic theory for which all logical bits are equivalent must be self-dual.
Quantum theory has the remarkable feature of self-duality: states and measurement outcomes are described (up to normalization) by the exact same mathematical objects. Here, we prove that this feature is a consequence of bit symmetry: any probabilistic theory for which all logical bits are equivalent must be self-dual.
Stationary algorithmic probability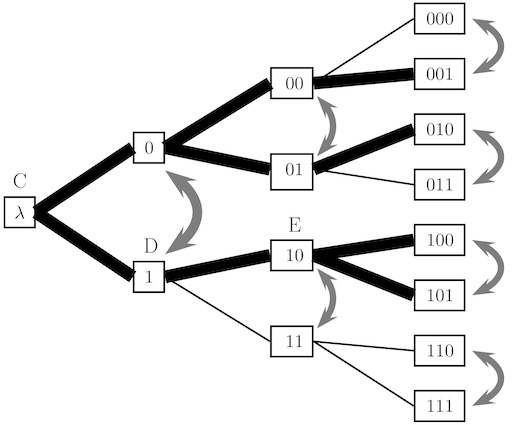 Kolmogorov complexity and algorithmic probability are always defined relative to a choice of universal computer. Can we get rid of this machine-dependence? Here, I give a natural idea for how this might be accomplished, but prove that, in the end, it cannot because of the existence of computer viruses and computable symmetries.
Kolmogorov complexity and algorithmic probability are always defined relative to a choice of universal computer. Can we get rid of this machine-dependence? Here, I give a natural idea for how this might be accomplished, but prove that, in the end, it cannot because of the existence of computer viruses and computable symmetries.
Quantum measurement occurrence is undecidable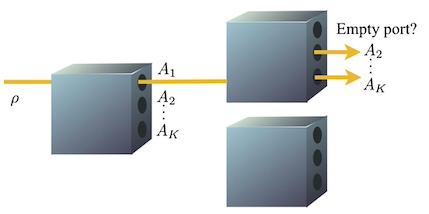 We show that a simple problem of quantum information theory is formally undecidable — that is, there does not exist any algorithm that determines the answer in all cases in a finite amount of time. Importantly, the analogous classical problem is (difficult, but) decidable.
We show that a simple problem of quantum information theory is formally undecidable — that is, there does not exist any algorithm that determines the answer in all cases in a finite amount of time. Importantly, the analogous classical problem is (difficult, but) decidable.
Strongly Universal Quantum Turing Machines and Invariance of Kolmogorov Complexity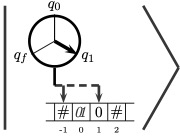 We prove a key result for the development of a quantum version of Kolmogorov complexity: we show that there are quantum Turing machines that simulate every other QTM, and halt exactly with probability one if the simulated machine does so.
We prove a key result for the development of a quantum version of Kolmogorov complexity: we show that there are quantum Turing machines that simulate every other QTM, and halt exactly with probability one if the simulated machine does so.
Law without law: from observer states to physics via algorithmic information theory An approach to the foundations of physics in which not an external world, but a mathematical notion of the first person (“self”) is fundamental. The goal is not philosophical contemplation, but concrete predictions for puzzling thought experiments on physics, agents, computation, and cosmology. More here.
An approach to the foundations of physics in which not an external world, but a mathematical notion of the first person (“self”) is fundamental. The goal is not philosophical contemplation, but concrete predictions for puzzling thought experiments on physics, agents, computation, and cosmology. More here.
Spin-bounded correlations: rotation boxes within and beyond quantum theory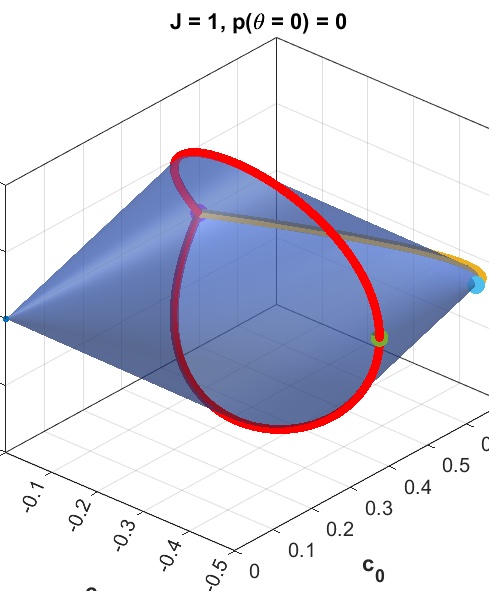 How can probabilities of events respond to spatial rotations, in any physical theory? We show that quantum theory admits all possible rotational correlations for spins 0, 1/2, and 1, but there are metrological games that can be won with higher probability via beyond-quantum spin-3/2 systems.
How can probabilities of events respond to spatial rotations, in any physical theory? We show that quantum theory admits all possible rotational correlations for spins 0, 1/2, and 1, but there are metrological games that can be won with higher probability via beyond-quantum spin-3/2 systems.
Entanglement-Asymmetry Correspondence for Internal Quantum Reference Frames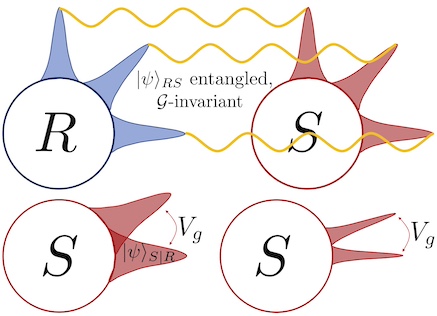 The Page-Wootters mechanism replaces background time by quantum correlations with a clock. Here we prove that the amount of entanglement with the clock tells us exactly how much time asymmetry is induced in the system, and this holds more generally for arbitrary symmetries and quantum reference frames.
The Page-Wootters mechanism replaces background time by quantum correlations with a clock. Here we prove that the amount of entanglement with the clock tells us exactly how much time asymmetry is induced in the system, and this holds more generally for arbitrary symmetries and quantum reference frames.
Higher-order interference and single-system postulates characterizing quantum theory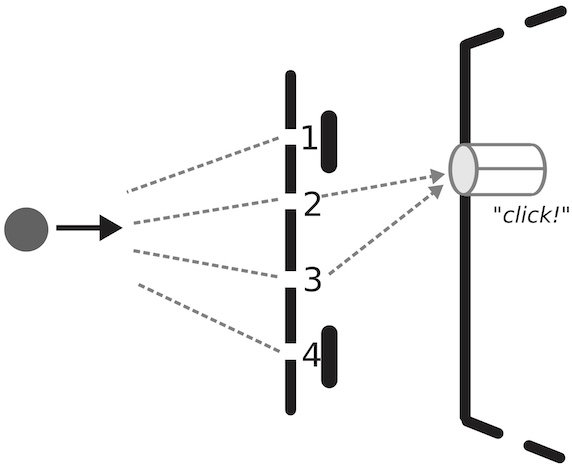 We derive quantum theory from four postulates that only refer to single systems, and not to composition: Spectrality, Strong Symmetry, No 3rd-order Interference, and Energy Observability.
We derive quantum theory from four postulates that only refer to single systems, and not to composition: Spectrality, Strong Symmetry, No 3rd-order Interference, and Energy Observability.
Thermalization and Canonical Typicality in Translation-Invariant Quantum Lattice Systems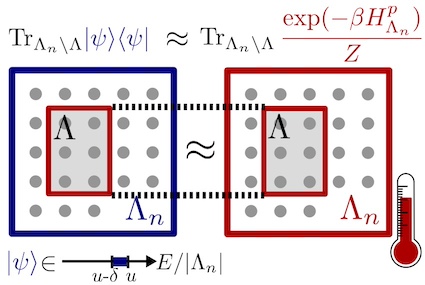 We give a rigorous proof of thermalization from entanglement: for translation-invariant quantum systems, almost all pure global states with large enough energy spread are locally for most times close to a Gibbs state.
We give a rigorous proof of thermalization from entanglement: for translation-invariant quantum systems, almost all pure global states with large enough energy spread are locally for most times close to a Gibbs state.
Stochastic Independence as a Resource in Small-Scale Thermodynamics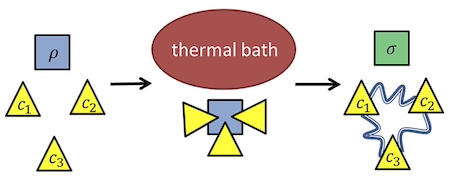 We show that creating correlations between initially uncorrelated systems can enable otherwise impossible state transitions in the resource theory of thermodynamics — the exact opposite of what one might naively expect with standard intuition.
We show that creating correlations between initially uncorrelated systems can enable otherwise impossible state transitions in the resource theory of thermodynamics — the exact opposite of what one might naively expect with standard intuition.
Concentration of Measure for Quantum States with a Fixed Expectation Value![]() We use integral geometry and techniques by Gromov to prove that almost all pure quantum states with a fixed (say, energy) expectation value behave similarly to the ensemble mean. This has important implications for the quantum thermodynamic behavior of such ensembles.
We use integral geometry and techniques by Gromov to prove that almost all pure quantum states with a fixed (say, energy) expectation value behave similarly to the ensemble mean. This has important implications for the quantum thermodynamic behavior of such ensembles.
Earlier Works
Fractional sums: how to add a non-integer number of terms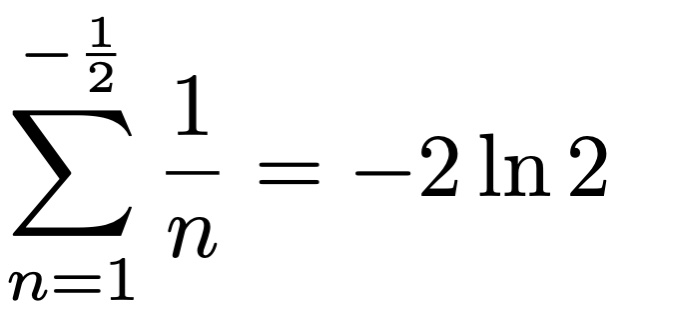 As a teenager, I developed a theory that extends the definition of sum series to a non-integer number of terms. This works surprisingly well, and leads to beautiful relations to special functions and constants.
As a teenager, I developed a theory that extends the definition of sum series to a non-integer number of terms. This works surprisingly well, and leads to beautiful relations to special functions and constants.
Debunking an alleged “antigravity” experiment In 1997, an American inventor (John Schnurer) claimed to have found a simple way to shield gravity with a superconductor. We reproduced his experiment and found that he seems to have mis-interpreted a simple buoyancy effect.
In 1997, an American inventor (John Schnurer) claimed to have found a simple way to shield gravity with a superconductor. We reproduced his experiment and found that he seems to have mis-interpreted a simple buoyancy effect.
Iterating the logistic map a non-integer number of times, and higher-order operations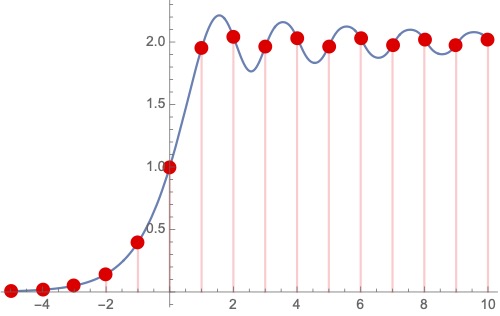 One often studies chaotic behavior by iterating a function a finite number (n=1,2,3, …) of times. As a teenager, I found a natural way to extend this to non-integer n.
One often studies chaotic behavior by iterating a function a finite number (n=1,2,3, …) of times. As a teenager, I found a natural way to extend this to non-integer n.